En este artículo, quiero compartir con vosotros una manera muy diferente de acercarse al riesgo de una cartera de inversión. Este enfoque lo aprendí de Oscar Gil Flores, quien tuve la suerte de tener de profesor en el IEB (Instituto de Estudios Bursátiles).
Lo que vamos a hacer es presentar el riesgo de una cartera como la suma de dos vectores: uno que corresponderá al riesgo sistemático y el otro, al no sistemático.
Esta descomposición nos ayudará a visualizar estos dos riesgos de una manera sencilla, al mismo tiempo que nos dirá con exactitud el alpha que genera el gestor en función del riesgo adicional en el que incurre para alcanzarlo. A esta ratio la llamaremos “ratio de Gil” que, en esencia, es una adaptación de la “ratio de información” pero más intuitiva y sencilla que ésta.
Rentabilidad y volatilidad
Cuando analizamos una cartera hay dos parámetros esenciales que siempre debemos analizar: su rentabilidad y volatilidad.
La rentabilidad es el rendimiento de esa cartera en función del capital invertido, y la volatilidad es el proxi académico para determinar el riesgo incurrido, y no es más que la desviación típica, es decir, la dispersión de las rentabilidades de la cartera respecto de su rentabilidad media.
A modo de ejemplo, calculemos la rentabilidad y la volatilidad de la siguiente cartera compuesta por cinco activos. Tenemos su rentabilidad, volatilidad y peso de cada uno dentro de la cartera:
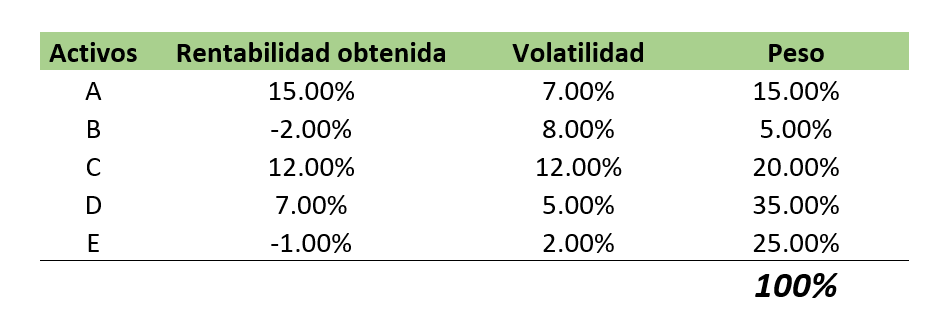
La rentabilidad de la cartera la calculamos mediante la suma ponderada de la rentabilidad de cada activo:
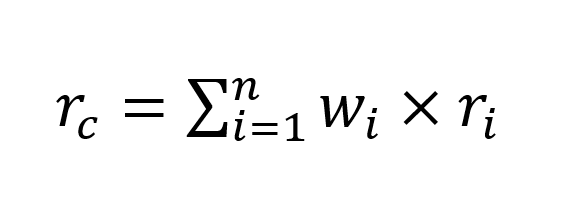
En nuestro ejemplo:
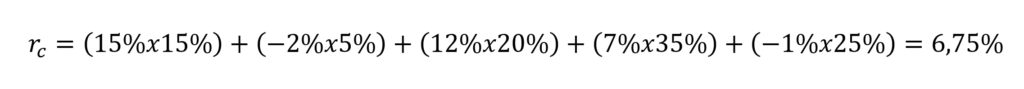
En Excel podemos utilizar la fórmula +SUMAPRODUCTO o utilizar Matrices con la fórmula +MMULT(TRANSPONER(RangoPeso);RangoRentabilidades).
Ahora calculemos la volatilidad, pero cuidado porque no podemos hacer la suma ponderada. Lo siguiente es un error
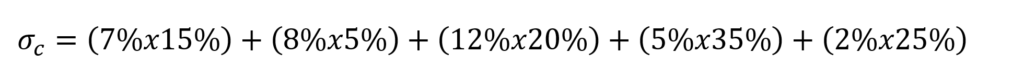
No se hace así porque la volatilidad no solo depende de las volatilidades individuales de cada activo y de su peso dentro de la cartera, sino que también de la interrelación que tengan los activos entre sí, es decir, de las correlaciones entre unos y otros.
Al cálculo anterior le faltan, por lo tanto, las correlaciones entre los distintos activos que componen la cartera.
La volatilidad es la desviación típica (σ), y la desviación típica es la raíz cuadrada de la varianza, y la varianza se calcula con la siguiente fórmula:
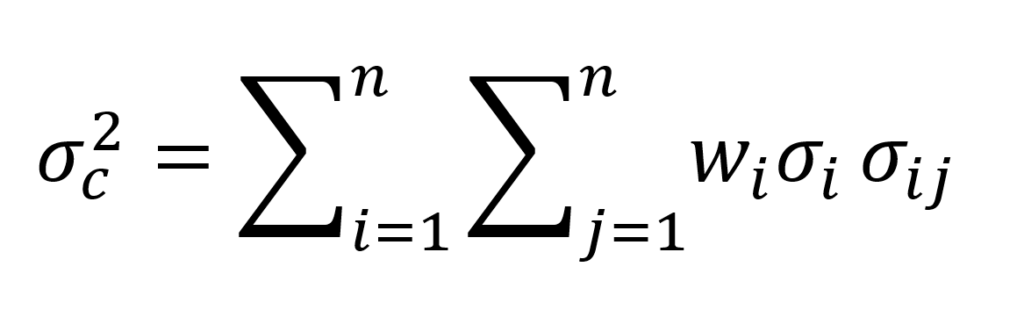
Cuando tenemos calculada la varianza, solo tenemos que calcular la raíz y ya tenemos la volatilidad.
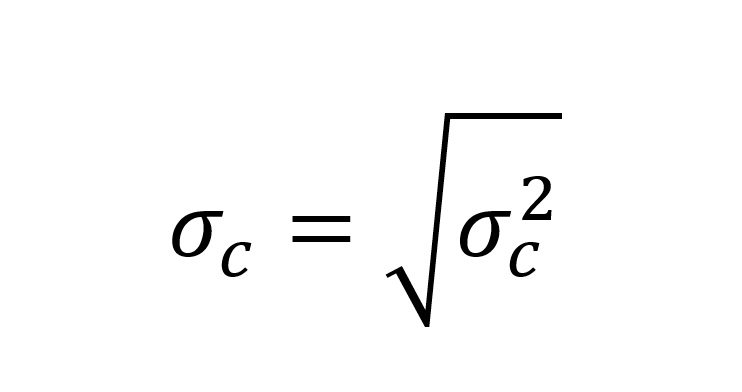
En la ecuación de la varianza, “w”, que es el peso de cada activo dentro de la cartera; “σ”, es la volatilidad de cada activo; y “σij”, la covarianza entre cada par de activos, siendo la covarianza igual a:

Esta fórmula es fácil de entender cuando la aplicamos a dos activos.
Supongamos una cartera compuesta por los activos (A y B), con sus datos correspondientes de rentabilidad, riesgo (volatilidad), peso dentro de la cartera y correlación entre ambos.

La rentabilidad la calculamos:
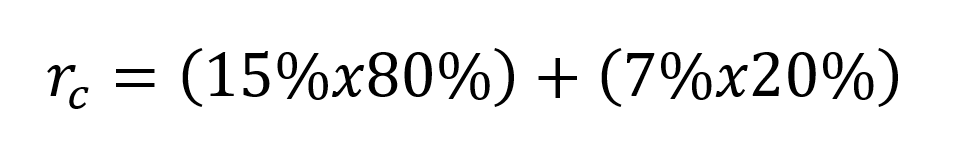
Y la volatilidad la calcularemos con la varianza a la que le aplicaremos la raíz cuadrada:
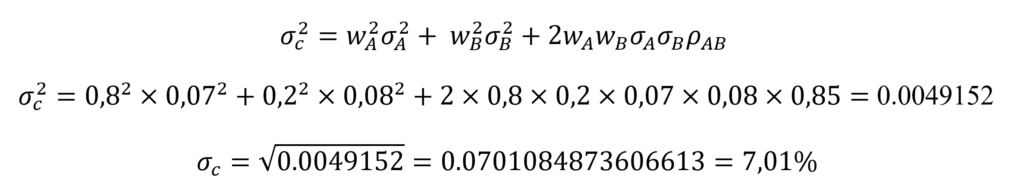
Como se puede ver, la volatilidad de la cartera no es la suma ponderada de las volatilidades individuales (que hubiese resultado de 7,20%) sino algo más complejo que dependerá también de la correlación entre ambos activos.
Volvamos al ejemplo de la cartera con cinco activos.
En principio, con los datos facilitados no podemos calcular la volatilidad de la cartera, ya que no teníamos el dato correlación entre los diferentes activos, pero imaginemos que son los siguientes:
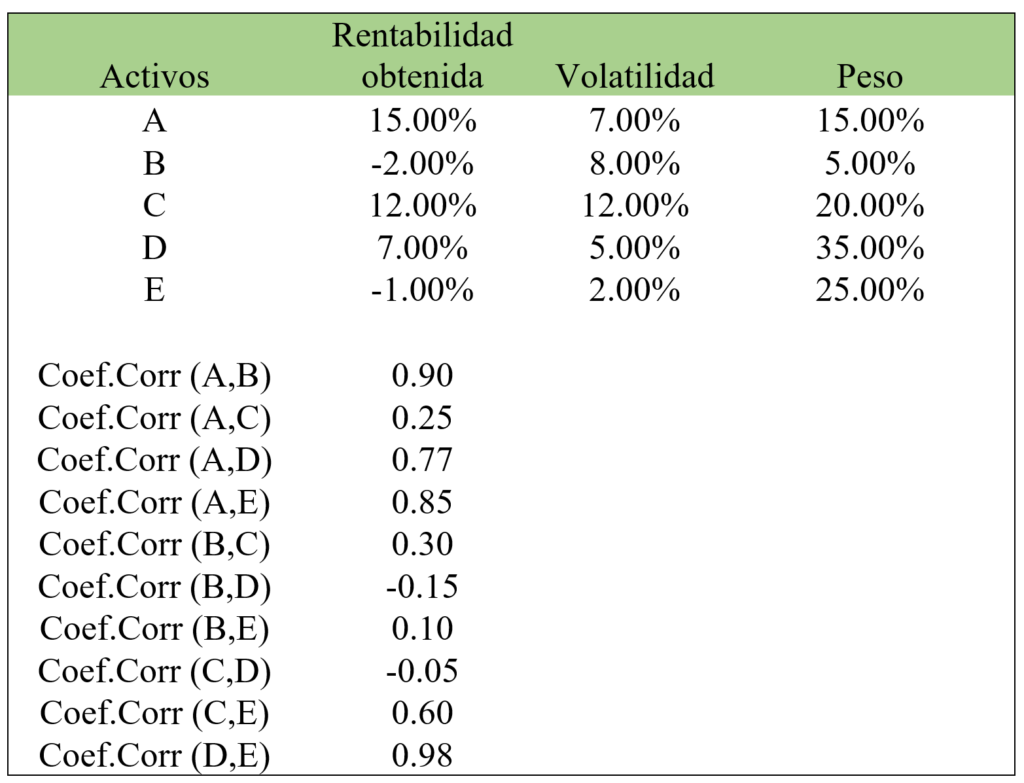
Ahora sí que podemos hacer nuestros números. Primero, las covarianzas con la fórmula anterior:
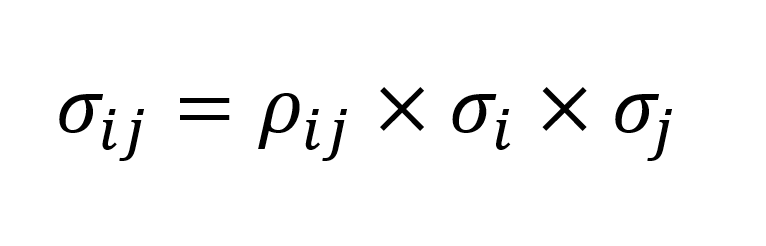
Y con esto podremos construir lo que se conoce como matriz “Varianzas-Covarianzas”, que es la usaremos en Excel para terminar de calcular la volatilidad de la cartera.
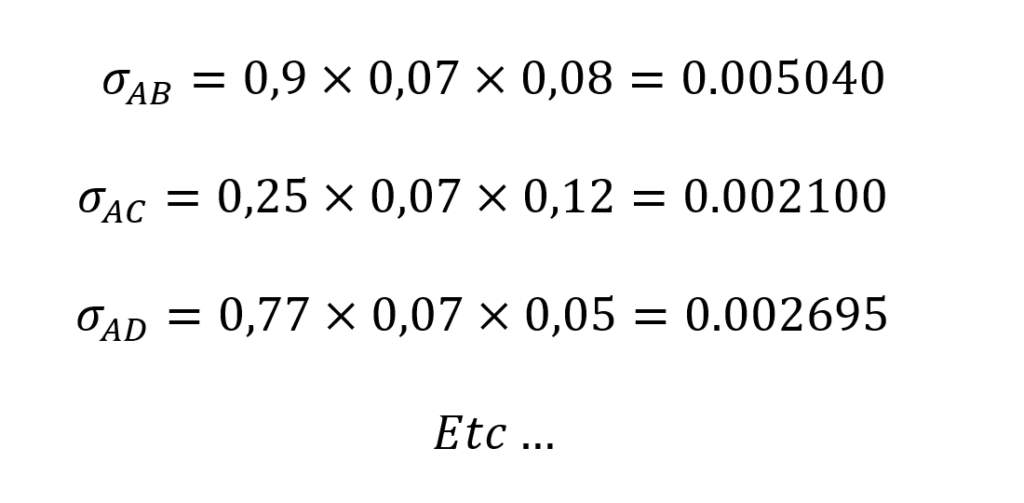
También calculamos la covarianza de A con A, de B con B, de C con C, de D con D y de E con E. Como el coeficiente de correlación de un activo consigo mismo siempre es uno, tenemos que:
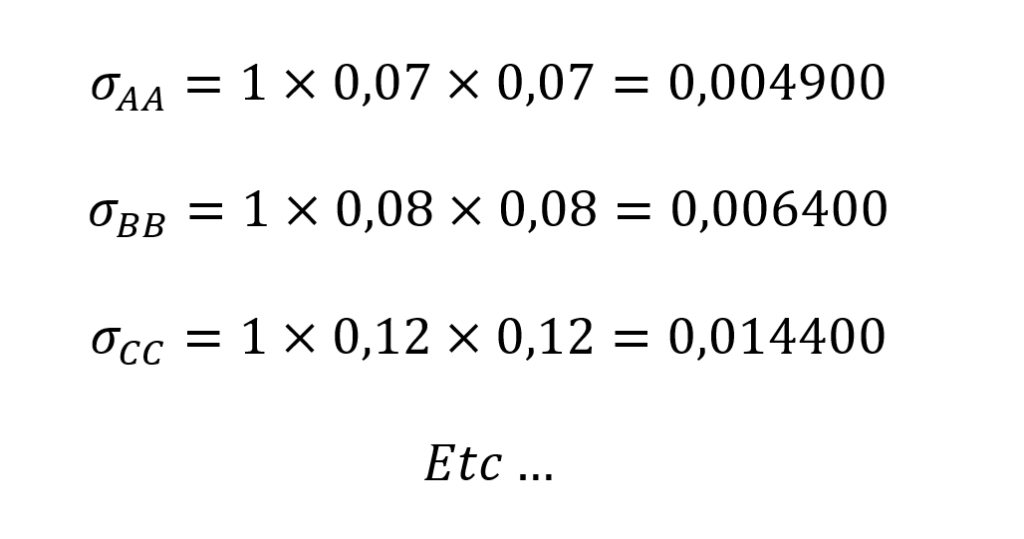
La matriz final queda así:
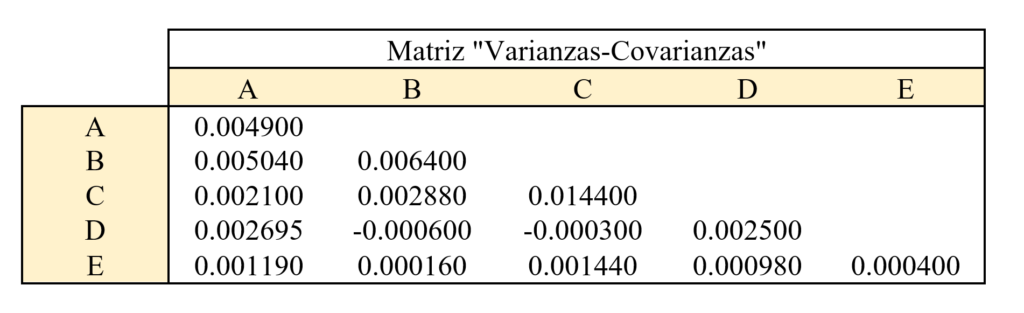
La matriz se calcula con Excel usando las cotizaciones históricas de los activos. Primero, calculamos las rentabilidades diarias. Y luego, con la función “Análisis de Datos” > “Covarianza”, obtenemos la matriz “Varianza-Covarianza”.
Cuando tenemos la matriz, la multiplicamos por el peso de cada activo con la fórmula:
=MMULT(MMULT(TRANSPONER(D2:D6);G3:K7);D2:D6)
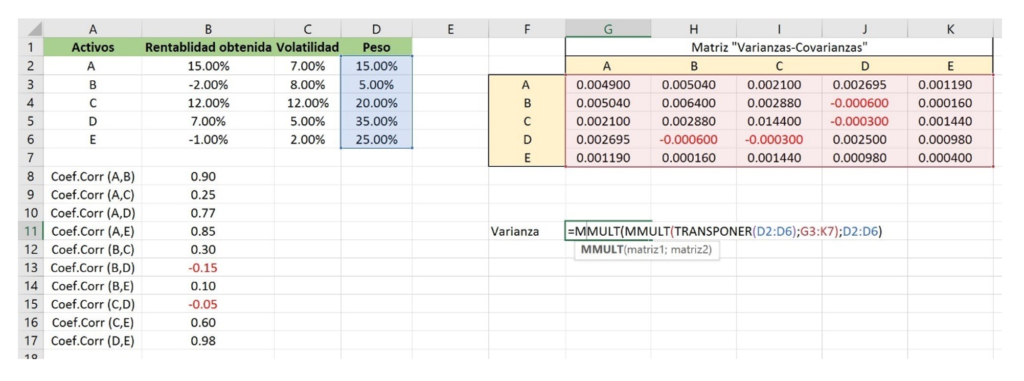
Así obtenemos la varianza. Y si le realizamos raíz cuadrada, llegamos a la volatilidad.
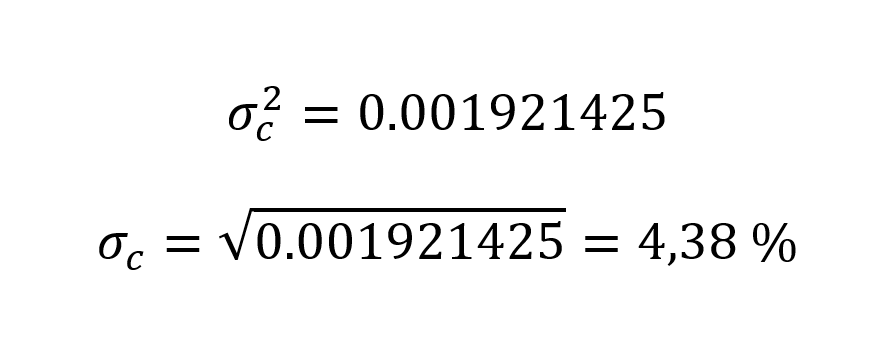
Fácil, ¿no?
Recapitulemos:
- La rentabilidad y la volatilidad son dos variables útiles para medir el desempeño de una cartera.
- La rentabilidad es fácil de calcular: sólo hay que hacer la suma de las rentabilidades de cada activo que compone la cartera ponderada por su peso en la cartera. Pero para calcular la volatilidad necesitamos conocer, aparte de la volatilidad de cada activo y su peso en la cartera, el coeficiente de correlación de cada par de activos, o mejor, sus covarianzas, ya que Excel nos permite obtener la matriz de “varianzas-covarianzas” de un tirón con el histórico de cotizaciones de los activos.
Riesgo sistemático y no sistemático.
La volatilidad calculada (4,38%) es el “riesgo total de la cartera”, pero realmente ese riesgo lo podemos descomponer en dos riesgo: el riesgo propio de cada activo y el riesgo propio del mercado donde cotizan dichos activos. Al primero lo llamamos “riesgo no sistemático” y al segundo, “riesgo sistemático”.
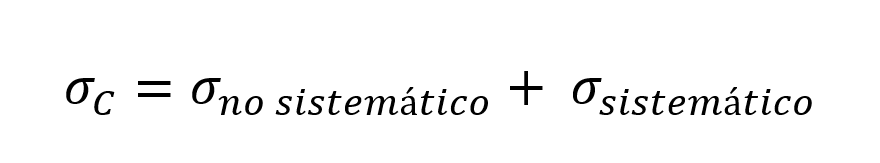
Lo mismo podemos decir de la rentabilidad. El 6,75% calculado es la rentabilidad total de la cartera, que también podemos descomponer en una componente “sistemática”, y en otra “no sistemática:
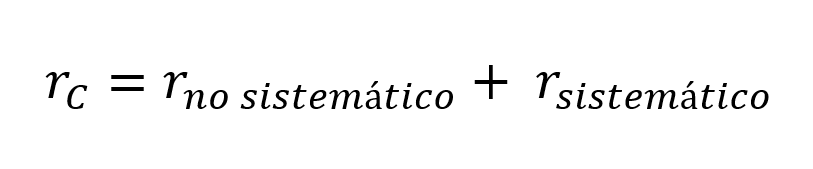
La pregunta es doble ¿Qué parte de ese 4,38% es riesgo sistemático y qué parte es riesgo “no sistemático”? Y, ¿qué parte de ese 6,75% de rentabilidad es sistemática y cuál es la no sistemática?
Imaginemos que analizamos una cartera de acciones españolas que obtuvo un 5% de rentabilidad con una volatilidad del 10%. Y sabemos que el Ibex35, en el mismo periodo, se revalorizó un 3%. A priori, parece que el gestor hizo un buen trabajo: ganó un 2% más que el índice. Pero supongamos que sabemos que, de ese 10% de riesgo asumido para obtener el 5%, un 3% corresponde a “riesgo sistemático” y un 7% a “no sistemático”. Podemos afirmar, entonces, que el gestor incurrió en un riesgo adicional del 7% para sacar apenas un par de puntos más al índice.
¿Es esto un buen trabajo por parte del gestor?
Si se hubiese indexado al Ibex, habría ganado un 3% con una cómoda volatilidad del 3%. Sin embargo, prefirió jugársela asumiendo una volatilidad extra del 7% con la que sólo pudo sacar un 2% de rentabilidad adicional.
¿Mereció la pena tanto riesgo para sólo un 2%?
Responder a esto dependerá de cada uno y de otras variables, pero qué duda cabe que descomponiendo la rentabilidad y la volatilidad en su parte sistemática y no sistemática obtenemos una información muy útil para valorar el desempeño de un gestor o de una estrategia de inversión concreta.
Beta y Alpha de una cartera
La beta es una métrica que nos ayuda a valorar en qué medida un activo (o una cartera) se ve afectado por las “turbulencias” del mercado. Es decir, en qué medida se ve afectando por el componente sistemático.
Una cartera poco sensible al mercado se verá poco afectado por éste. Si es muy sensible, cualquier cambio del mercado le afectará sustancialmente.
La beta es, en esencia, la exposición al mercado que asume el gestor de una cartera.
- Si una cartera tiene una beta de 1 (=1) querrá decir que, si el índice de referencia (el mercado) sube un 1%, nuestra cartera subirá también un 1%. Es decir, se mueve a la par del mercado, con la misma intensidad.
- Si la beta es mayor que uno (=1,2, por ejemplo), si el mercado sube un 1%, nuestra cartera subirá un 1,20%.
- Y si la beta es menor que 1 (= 0,80, por ejemplo), si el mercado sube un 1%, nuestra cartera subirá un 0,80%.
Las carteras (o activos) con betas mayores de uno son carteras agresivas; las que tienen betas iguales a uno, moderadas; y menores que uno, conservadoras.
Esta dependencia de la cartera al mercado (medida por la beta) es un elemento troncal de la valoración los activos por el modelo CAPM (Capital Asset Princing Model)
El modelo CAPM postula que la rentabilidad de una cartera viene determinada por la siguiente fórmula:

RLR es la rentabilidad Libre de Riesgo; β es la beta; y «α» el exceso de rentabilidad sobre el mercado obtenida por el gestor.
Según el modelo CAPM, la rentabilidad de la cartera dependerá tanto de la beta como de la alpha.
Un buen gestor de activos debe perseguir rentabilidades que superen a las del mercado, pero obtenidas con alpha, no asumiendo betas mayores a uno.
Si queremos conocer el alpha de un gestor, sólo tenemos que despejar de la fórmula anterior:
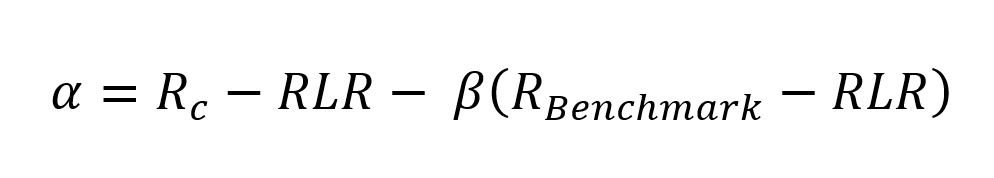
Imaginemos una cartera con tres activos: Iberdrola, Telefónica e Inditex. Iberdrola pesa un 40% en el total de la cartera, Telefónica, un 35% e Inditex, un 25%. Hacemos nuestros cálculos (en Excel) y calculamos la beta de cada uno: beta de Iberdrola, 0,9; Telefónica, 1; e Inditex, 1,3.
La beta de la cartera será:
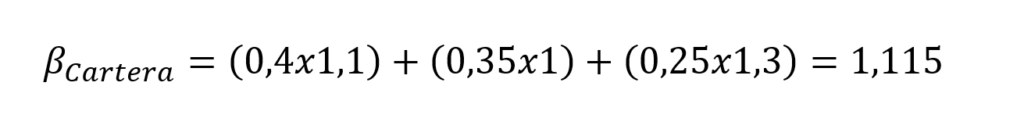
¿Cómo hemos calculado la beta de estos activos individuales? Muy fácil:
- Nos descargamos el histórico de cotizaciones de cada activo, y los del índice de referencia (benchmarck), por ejemplo, de los últimos cinco años.
- Calculamos las rentabilidades diarias.
Sobre las rentabilidades, calculamos la covarianza entre el mercado y el título, y la varianza del mercado, y resolvemos la siguiente ecuación:
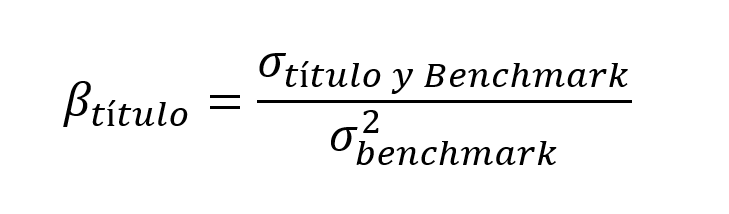
En Excel, la covarianza entre el título y el Benchmark se calcular con la función +COVARP(;) y la varianza del Benchmark con la función +VARP().
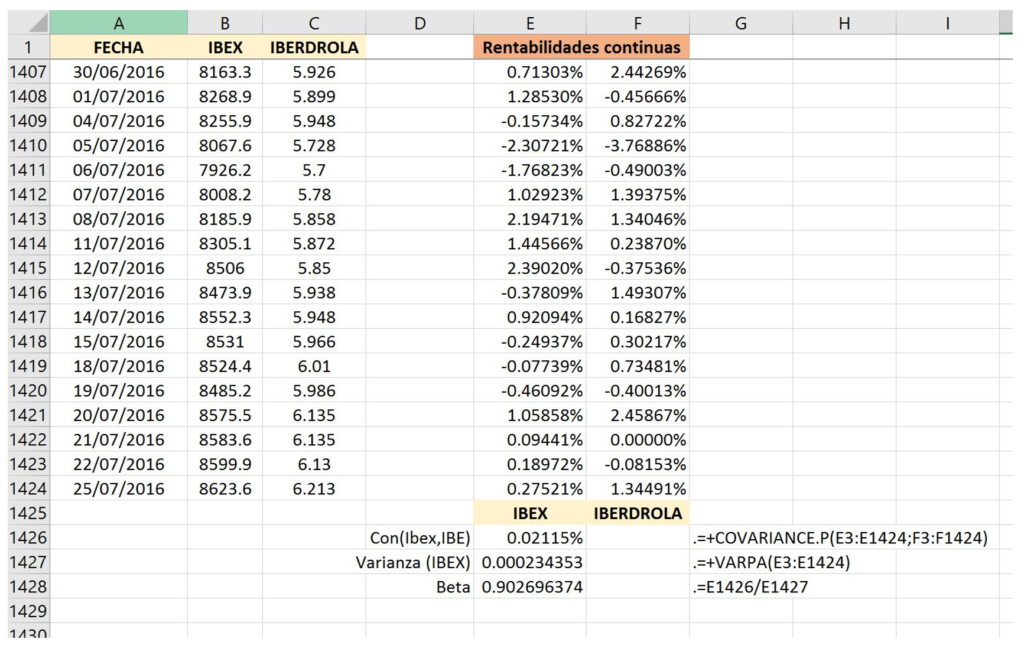
La imagen anterior es un pantallazo de los cálculos para calcular la beta de Iberdrola, desde enero del 2011 hasta 2018.
Las rentabilidades diarias están calculadas con la siguiente fórmula:
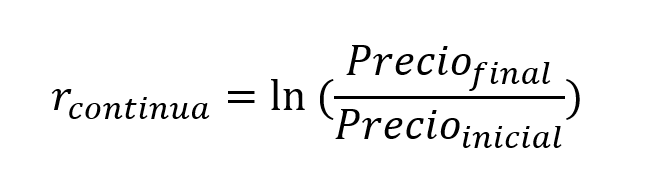
Para visualizar la relación entre Iberdrola y el índice de referencia (el Ibex), podemos construir un gráfico de dispersión como el siguiente:
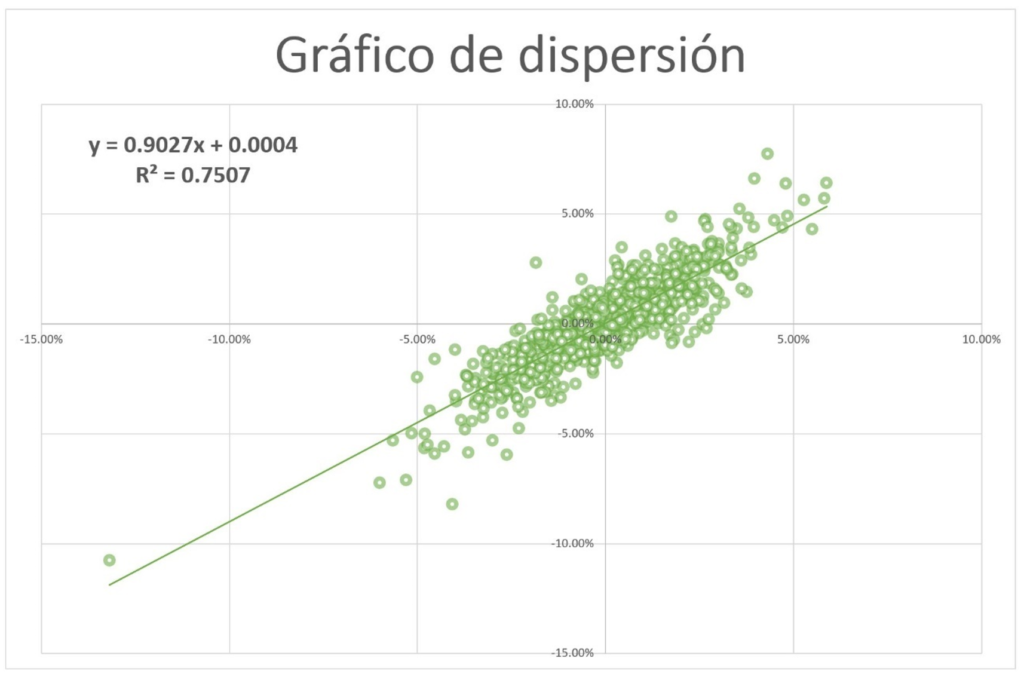
Si a este gráfico, le sacamos la ecuación de su recta, observamos como la pendiente es precisamente la beta calculada.
Recapitulemos:
- Dijimos que había dos variables muy importantes para analizar la gestión de una cartera: la rentabilidad y la volatilidad.
- La volatilidad es sinónimo de riesgo en términos académicos.
- Las rentabilidades se suman linealmente, pero los riesgos no. La rentabilidad de la cartera es fácil de calcular porque es la suma ponderada de las rentabilidades de los activos que la componen. Sin embargo, la volatilidad depende de la correlación que tengan entre sí dichos activos.
- El riesgo total de la cartera se puede descomponer en dos riesgos distintos: riesgo no sistemático y riesgo sistemático. El primero es el intrínseco a las compañías que componen la cartera. Y el segundo, el propio del mercado donde negocian los activos.
- La sensibilidad de una cartera al riesgo sistemático es la beta. Betas mayores de 1 se consideran títulos o carteras agresivas. Betas iguales a uno, serán carteras que fluctúen en magnitudes idénticas al índice. Y betas menores a uno serán carteras moderadas o menos “riesgosas” en términos de sensibilidad al mercado.
- Todo lo que un gestor es capaz de conseguir más allá de la rentabilidad de su benchmark condicionado por la beta es lo que se conoce como alpha.
Representación gráfica de la descomposición del riesgo total: riesgo sistemático y no sistemático.
¿Cómo podríamos representar gráficamente esa descomposición del riesgo total de una cartera, en su parte sistémica y en su parte no sistémica? Como una suma de vectores.
Imaginemos que tenemos los siguientes datos de rentabilidad y riesgo de una cartera, y de su Benchmark:

Como la Tasa Libre de Riesgo es del 1%, la verdadera rentabilidad de la cartera no un 10%, sino un 9%, ya que un 1% lo podemos obtener sin asumir ningún tipo de riesgo. Es decir, la rentabilidad que obtiene la cartera asumiendo riesgo (volatilidad del 15%) es del 9%, no del 10% ya que hay un 1% que corresponde a la tasa libre de riesgo que no tiene riesgo (volatilidad es igual a cero). Y el benchmark, un 8% asumiendo un 12% de volatilidad.
Representemos la volatilidad de la cartera y la del Benchmark como vectores:
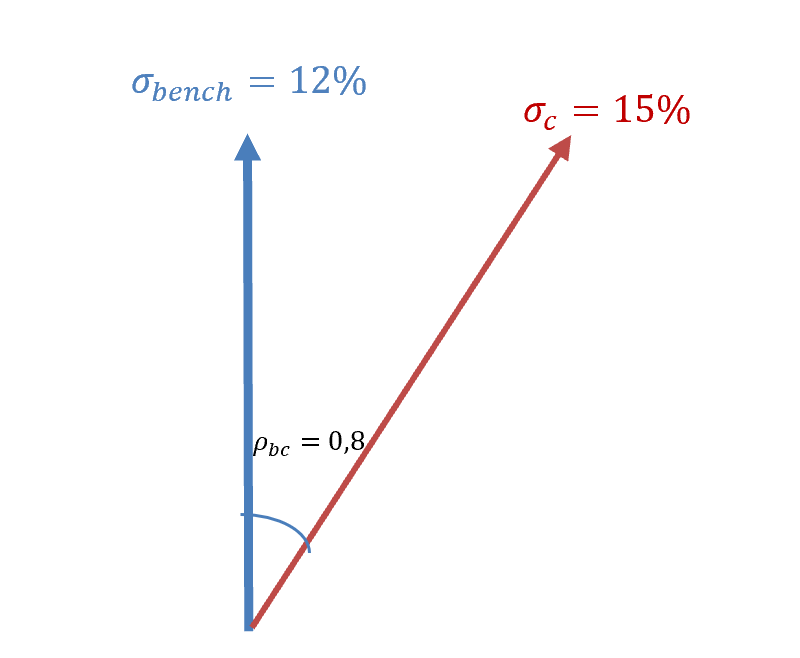
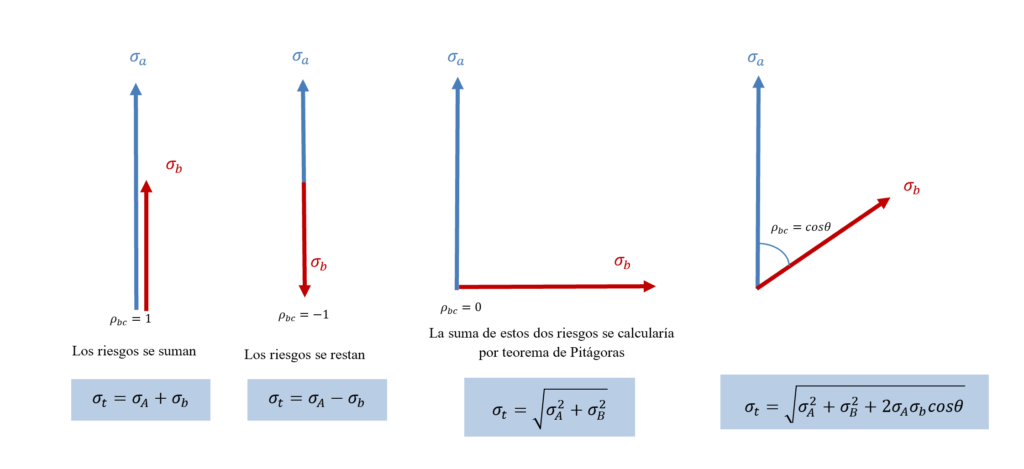
El coeficiente de correlación es el ángulo que separa los dos vectores.
Si la correlación hubiese sido igual a uno, los dos vectores hubiesen estado completamente alineados. En este caso, sus riesgos sí pueden sumarse linealmente.
Si la correlación fuera menor a uno, tendríamos dos vectores completamente opuestos, y sus riesgos se restarían.
Si la correlación es igual a cero, tenemos dos vectores que nada tienen que ver: uno va para un lado y el otro va para el otro. Y para calcular la suma tendríamos que utilizar el Teorema de Pitágoras, que nos dice que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Y si los dos forman un ángulo (el ángulo es el coeficiente de correlación) utilizamos la fórmula que ya conocemos.
Volvamos al ejemplo.
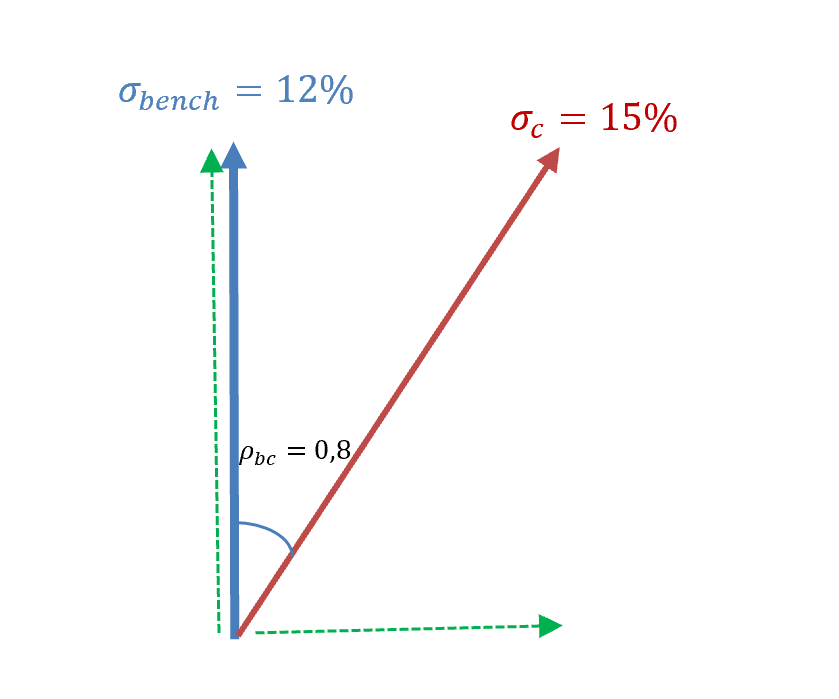
Dijimos que el riesgo de una cartera lo podíamos descomponer en riesgo sistemático y en riesgo no sistemático. Esta descomposición la podemos representar con un vector alineado con el riesgo del Benchmark (riesgo sistemático) y otro perpendicular, completamente independiente, que corresponderá al riesgo “no sistemático”. Dibujamos estos dos vectores en color verde: el vertical será el sistemático y el horizontal el no sistemático.
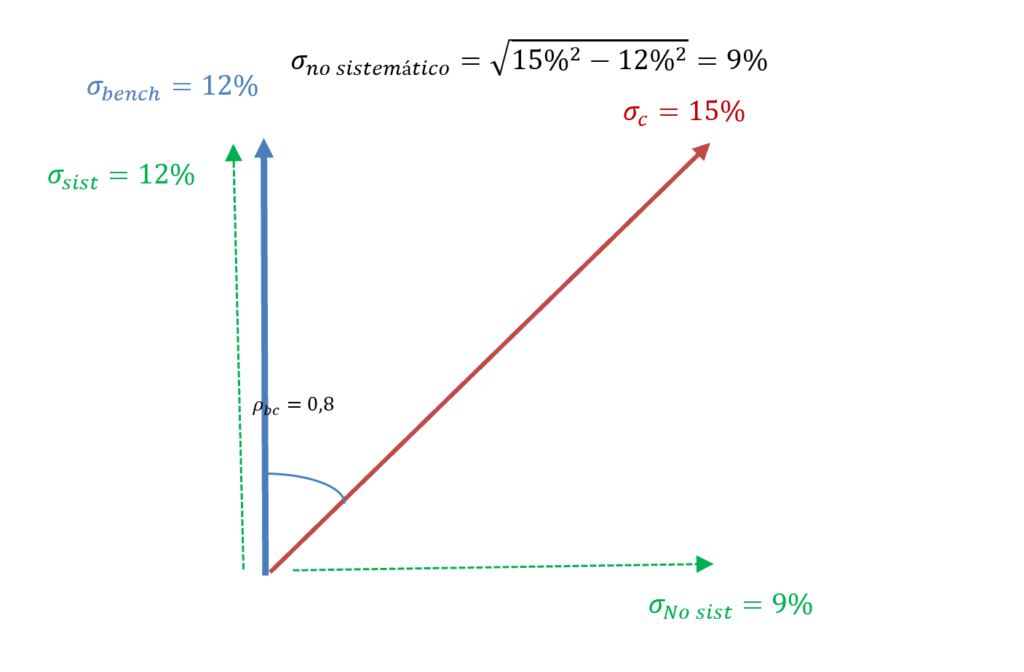
La altura del vector perpendicular (riesgo sistemático) será igual a la correlación (0,8) por el 15%, que es la volatilidad de la cartera. Es decir, un 12%. Y el cálculo de la parte no sistemática lo haremos con el Teorema de Pitágoras, siendo el 15% la hipotenusa y el 12% uno de los catetos. Despejamos y:
Lo que acabamos de hacer es descomponer el riesgo total de la cartera en un vector alineado con el riesgo del mercado y en otro completamente independiente.
La pregunta que nos podemos hacer es: de la rentabilidad del 9% que obtuvo la cartera ¿qué porcentaje viene de la flecha verde vertical y qué porcentaje viene de la flecha horizontal? Es decir, ¿qué porcentaje es atribuible al riesgo sistemático y qué porcentaje es atribuible al riesgo no sistemático?
Este es el verdadero meollo de la cuestión. No se trata de si el gestor fue capaz de sacar una rentabilidad del 9%, sino cuánta rentabilidad fue capaz de obtener asumiendo riesgo no sistemático (representado por la flecha verde horizontal).
Es el 9% de rentabilidad la que queremos descomponer en su parte sistemática y no sistemática.
La proporción de la parte sistemática (flecha verde vertical), junto con la flecha azul que es la del benchmark, la determina la beta. En este caso, como las magnitudes son exactamente las mismas (12%), la beta es 1. Si la flecha verde hubiese sido la mitad que la azul (6%), la beta hubiese sido de 0,5. Y si hubiese sido mayor, por ejemplo, un 16%, la beta hubiese sido de 1.33. Una mera regla de tres.
Sabemos, por lo tanto, que, si con un 12% de volatilidad y una beta de uno, el gestor obtuvo un 8% de rentabilidad total, a parte sistemática también debe ser de un 8% (8% x beta). Para calcular la parte no sistemática, como las rentabilidades si son lineales, sólo tenemos que despejar de la fórmula:
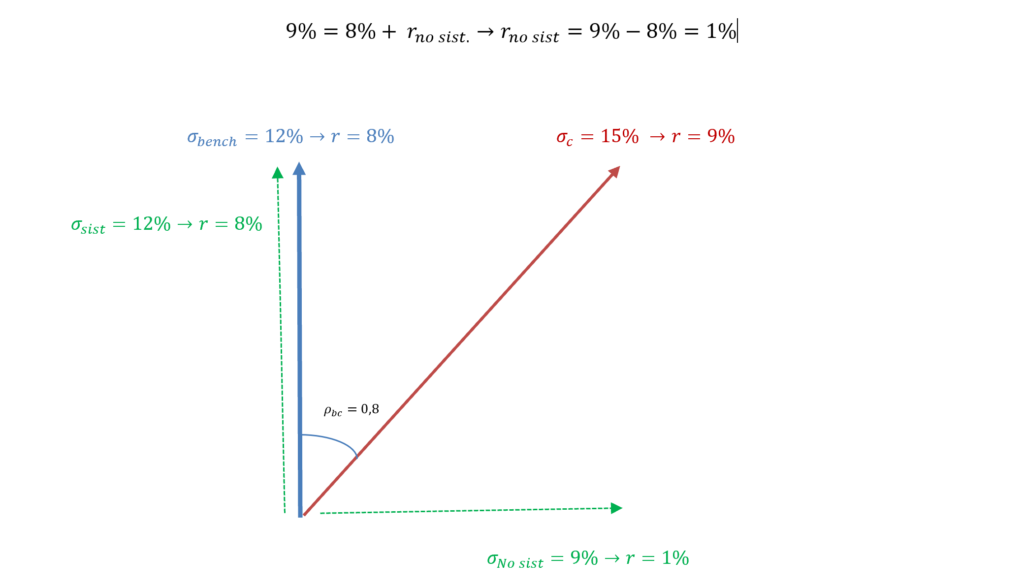
La rentabilidad no sistemática es del 1%. Esto quiere decir que el gestor ha logrado un 1% de alpha asumiendo un 9% de volatilidad no sistemática.
¿Cómo interpretamos esto? ¿Hizo el gestor una labor eficiente?
Para evaluar el desempeño de una cartera, la ratio más usada en la industria es la famosa ratio Sharpe, que, en nuestro ejemplo, queda de la siguiente manera:
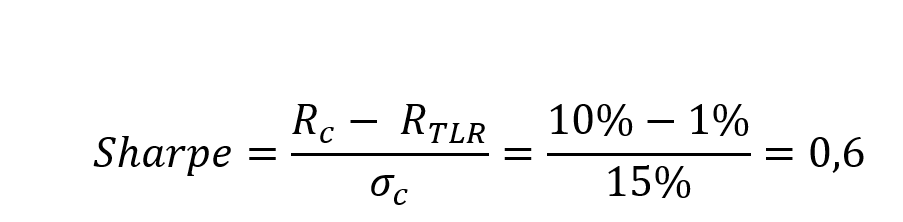
Pero la Sharpe se queda corta porque no diferencia entre rentabilidad y riesgo sistemático y no sistemática. No es una métrica, por lo tanto, demasiado precisa para comparar la labor profesional de dos gestores de activos. Pero ahora, una vez hemos descompuesto la rentabilidad y el riesgo, podemos fabricar una “Sharpe” más precisa que sólo tenga en cuenta la parte no sistemática. Ahora, podemos enfrentar el exceso de rentabilidad no sistemática (1%) contra el riesgo específico que asumió para obtener (9%). A esta Sharpe la llamaremos “ratio de Gil”, en honor a Óscar Gil.
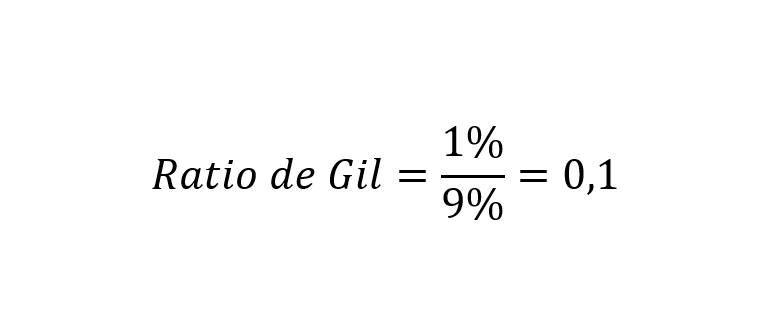
Observamos cómo la Gil es mucho más precisa. La Sharpe enfrenta el exceso de rentabilidad de la cartera frente de la tasa libre de riesgo contra el riesgo total, sin diferenciar qué parte es sistemática y qué parte es no sistemática. Sin embargo, la Gil evalúa sólo la rentabilidad mérito del gestor: Alpha Vs riesgo asumido para obtener esa alpha.
Conclusión
Medir el desempeño de un gestor profesional o de una cartera es un asunto importante. La Sharpe es una medida insuficiente por no diferenciar entre rentabilidad y riesgo sistemático y no sistemático. Con la ratio de Gil tenemos una alternativa sencilla y más que mide la eficiencia del Alpha en función de la volatilidad no sistemática.


Caray…un poco complicado….
Habrá que releer otra vez.
Algún apoyo audiovisual para ayudar a comprender estos temas?
Gracias por tomarse el tiempo de compartir.